In passing, hijacking is where one passer decides to change what pattern they are passing and their actions transitions their partner into a compatible pattern. One passer is making an active choice, the other is passively responding. All transitions involve changing how many clubs are being juggled locally by +/- 1 club (assuming the passive partner makes the minimal causal change). If the passer who is doing an active transition is gaining a club locally then the transition is a “hijack”, if the active transition loses a club locally then it is a “lowjack”. Collectively these are also known as “programming” because you are programming your partner. Most people use programming and hijacking interchangeably.
Hijacking started in 6 club period 5 patterns, these patterns are described in Aidan Burns’ Highgate collection https://passing.zone/wp-content/uploads/2016/01/highgate.pdf. If you are new to this type of pattern you should start with these (Aidan gives excellent instruction which I shall not repeat here, see page 36). However, the Highgate collection does not go into generalities about hijacking. Having become interested in these patterns and worked my way through all the publicly known hijacks I wanted to generate more of them and capture the general rules on what are the properties that make something a hijack.
General rules of hijacking for two passers
- If you have an empty hand because you did not receive a “pass”, zip into the empty hand
- If you were going to zip into a hand, but there is a pass coming to that hand throw a “pass” instead of a zip
- A “pass” is defined as the period of the pattern + 2 (e.g. in period 5 pattern a “pass” is a 7)
- The period of the pattern before and after the transition must be the same
- All patterns must have one or more passes (N.B. any pass satisfies this condition, not just period+2 “passes”)
- There can be 0 or 1 active transition throws (a “transition throw” is a throw which is not part of the pattern you are transitioning to or from)
- All throws made on the passive side must belong to a pattern they are transitioning to or from
- The passive responder must make a causally minimal change to their juggling in response to an active transition
- All global patterns of twice local period are valid 4 handed siteswaps (N.B. if all patterns valid the local period, each passer will always have an integer number of clubs locally. However, if patterns are only valid considering globals that are twice what we have been calling the local period then they are integer and half club patterns – I believe Brook has written one of these, but I have not passed it and I have no examples of such patterns in this post.)
These are a draft of the rules I have inferred from examples, the list may not be complete or accurate. If you have counter examples I would love to see them.
Patterns may have other passes that are not period + 2, but these are incidental; only a period + 2 “pass” is suitable for a hijacking transition. A corollary of these rules is that a transition results in one passer gaining a club locally, the other losing a club locally. If a transition is valid and fits these rules then it is part of the class of patterns that called “hijacks”. These rules are sufficient to determine if something is a hijack or not, so with enough brute force they could be considered generative in terms of filtering arbitrary causally valid strings of numbers, but I do not consider these rules to be well developed enough to be elegantly generative. While I hope to add to the rules, I would welcome somebody brute forcing a generator for hijacking transitions.
Notation for transitions
Much of the working out of the patterns is done in 4 handed global, however for describing transitions I have found it effective in workshops to write [pattern 1 in local]transition throw if any[pattern 2 in local] with the pattern 1 and pattern 2 written in the order required such that the entire string is what you do locally going through the transition. A corresponding string for the passive response appropriately offset is generally provided in workshops, although for my own notes I generally don’t bother as the passive responder will just respond naturally.
One nice thing that drops out of this notation is that it becomes clear that when the patterns are heterogeneous the minimal global is twice the length of the minimal when the pattern is homogeneous. This can be treated as a clue when it comes to considering how to go about representing these patterns when attempting to generate them automatically. Another little clue is when there is an active transition throw that does not belong to either pattern, which indicates that states of the patterns we are transitiong between are not the same – state diagrams/representations might be a good way to look at finding these transitions.
When I am working things out, my standard approach is to find the three (or four) patterns needed in global and once I have them I switch to locals and intuit what and where the transition is, and if there is a transition throw what that transition throw is. The absence of any formal process for this is something I would like to solve.
Due to the way I work with both local and global, I will sometimes be using numbers in local instead of hefflish.
Hijacking in period 3
If the period is 3, then the hijackable passes are zaps: 3+2=5. There was some concern that a zap might not be enough warning to know you aren’t going to have an empty hand, but that turned out not to be an issue.
855
The active passer here is hijacking, by throwing an 8 instead of a 5. There are no active (out of pattern) transition throws.
Transitioning out of 855
[855][885] active transition goes up 1 club (hijack)
[585][582] passive response goes down 1 club
The return transition
[885][855] active transition goes down 1 club (lowjack)
[582][585] passive response goes up 1 club
The is a minor variation, you can initially make either 5 into an 8 (transitioning from 855). However the same is not true of the return, the 5 you turned into an 8 to enter the pattern will dictate which of the 8s can be thrown as a 5 to make the return transition. Other than that, the two options are the same.
Holy grail 975
Holy hijacking Batman! is this pattern really easy enough to do hijacking in? Apparently it is.
Transitioning out of 975
[579][879] active transition goes up 1 club (hijack)
[957][927] passive response goes down 1 club
The return transition
[879][579] active transition goes down 1 club (lowjack)
[927][957] passive response goes up 1 club
Hijacking in period 5
If the period is 5, then the hijackable passes are singles: 5+2=7. Aidan’s two person hijacks fall into this category, so there was little new from me with 6 clubs in period 5. I was able to make an additional transition into Maybe on Aidan’s diagram to make a loop. There was also some prior work by Brook Roberts with 7 club patterns which has the exciting option of hijacking from 7 clubs to 8vs6 to 9vs5 locally.
Classic hijacks and the 6 club loop
Aidan wrote up the transitions for most of these in the highgate collection, with the only novel addition being the transitions between “Maybe” and “Popcorn Vs 5 club y not”. I’ve found it helpful to lay the patterns out in the following graphical relationship.
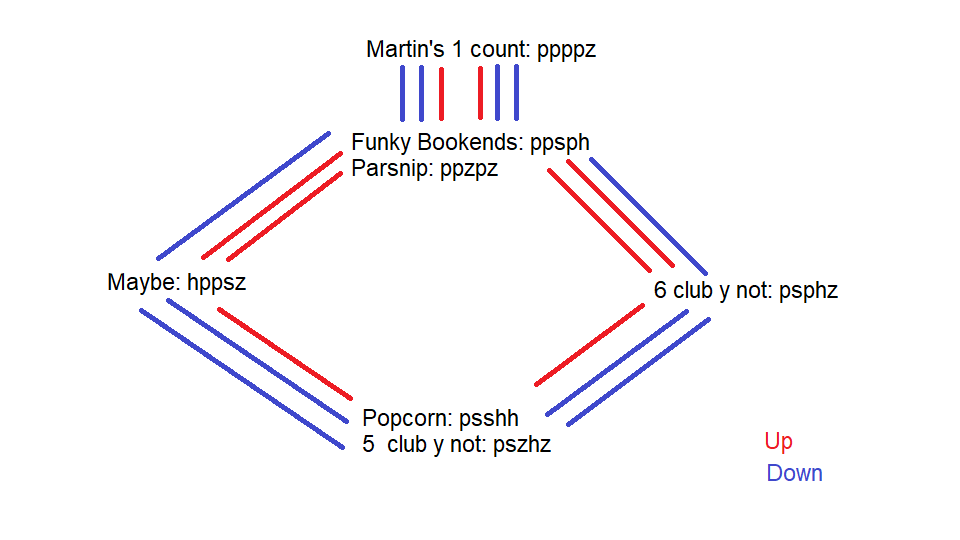
Figure 1. The vertical axis of this graph indicates the number of passes each pattern has, with 1 pass at the bottom and 4 passes at the top. “Up” and “Down” refer to increasing or decreasing the number of passes respectively. From each symmetric pattern there are two routes out as either passer may take the active role. Funky bookends vs parsnip has two transitions up to Martin’s one count, but only the funky bookends passer can make them. Martin’s one count has two different transitions (self or heff) back down to funky bookends vs parsnip, either passer may take either route down, so in total there are four ways of leaving this pattern.
This video covers the main loop from Maybe, up to Funky bookends vs parsnip down to 6 club y not, down Popcorn vs 5 club y not and up to Maybe again. Below is a list of all the transitions shown on figure 1, the transitions used in the video are marked with a *.
Maybe to Popcorn Vs 5 Club Y Not
[87762][88766] active transition goes up 1 club (hijack)
[62877][62827] passive response goes down 1 club
Popcorn Vs 5 Club Y Not to Maybe*
[87668][77628] active transition goes down 1 club (lowjack)
[28276][28776] passive response goes up 1 club
Maybe to Parsnip Vs Funky Bookends*
[62877]4[72772] active transition goes down 1 club (lowjack)
[77628][77678] passive response goes up 1 club
Parsnip Vs Funky Bookends to Maybe
[72772]4[87762] active transition goes up 1 club (hijack)
[76787][76287] passive response goes down 1 club
6 Club Y Not to Popcorn Vs 5 Club Y Not*
[76782][76688] active transition goes up 1 club (hijack)
[82767][82762] passive response goes down 1 club
Popcorn Vs 5 Club Y Not to 6 Club Y Not
[76688][76782] active transition goes down 1 club (lowjack)
[82762][82767] passive response goes up 1 club
6 Club Y Not to Parsnip Vs Funky Bookends
[82767]4[77272] active transition goes down 1 club (lowjack)
[67827][67877] passive response goes up 1 club
Parsnip Vs Funky Bookends to 6 Club Y Not*
[77272]6[76782] active transition goes up 1 club (hijack)
[78776][78276] passive response goes down 1 club
Parsnip Vs Funky Bookends to Martin’s one count A
[78776][77772] active transition goes down 1 club (lowjack)
[72727][72777] passive response goes up 1 club
Martin’s one count to Parsnip Vs Funky Bookends A
[77772][78776] active transition goes up 1 club (hijack)
[72777][72727] passive response goes down 1 club
Parsnip Vs Funky Bookends to Martin’s one count B
[77678][77772] active transition goes down 1 club (lowjack)
[72772][72777] passive response goes up 1 club
Martin’s one count to Parsnip Vs Funky Bookends B
[77772][77678] active transition goes up 1 club (hijack)
[72777][72772] passive response goes down 1 club
Going up into Martin’s one count and back down into funky bookends allows you to change which passer has the Parsnip side of the pattern. So, as well as being a little loop of its own, it also would allow you to change who is able to take the routes down from Parsnip. (no footage found)
Hijacking out of Funky Bookends with 7 clubs
Initially proposed by Brook and modified by me so that it is 5 club Y not at the bottom rather than 5 club not Y. This base pattern allows you to do 7 clubs each, 8 clubs vs 6 clubs and 9 clubs vs 5 clubs. Originally Brook had this going through 6 club y not. Based on my modifications to the 6 club loop I also looked for a Maybe version of this and was able to add it. I don’t believe any historical footage of the Brook’s original set of transitions through to 5 club not y exists, but Cameron and I had it running nicely in November 2018 (Leeds convention?) and didn’t film it because Cameron had to go an tech for the show.
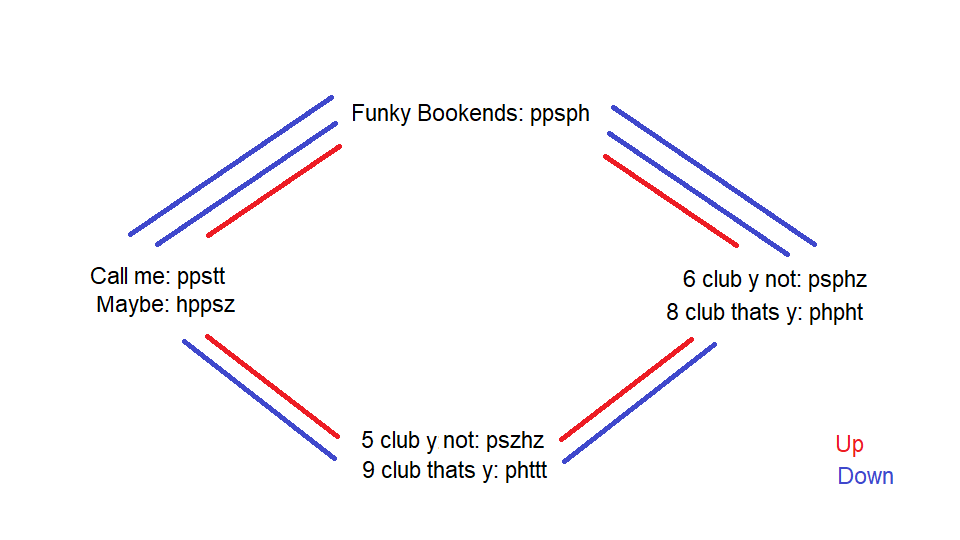
Figure 2. Transition diagram for hijacking in period 5 with 7 clubs from Funky Bookends through to 5 Club Y Not.
UP AND DOWN ON THE MAYBE SIDE
[embedyt] https://www.youtube.com/watch?v=67uRvFv7npw[/embedyt]
Preliminary work making sure we can go to 9 clubs vs 5 clubs through maybe as this side was brand new in Kerlingen. This is down and up on the left side of Figure 2.
THE SEVEN CLUB LOOP USING MAYBE AND 6 CLUB Y NOT
Funky Bookends to PHPHT vs 6 Club Y Not
[77678][A7878] active transition goes up 1 club (hijack)
[78776][78276] passive response goes down 1 club
PHPHT vs 6 Club Y Not to PHTTT vs 5 Club Y Not
[78A78][AAA78] active transition goes up 1 club (hijack)
[76782][76282] passive response goes down 1 club
PHPHT vs 6 Club Y Not To funky bookends
[A7878][77678] active transition goes down 1 club (lowjack) – transition not shown in either video
[78276][78776] passive response goes up 1 club
PHTTT vs 5 Club Y Not to PHPHT vs 6 Club Y Not
[AAA78][78A78] active transition goes down 1 club (lowjack) – transition not shown in either video
[76282][76782] passive response goes up 1 club
PHTTT vs 5 Club Y Not to PPSTT vs Maybe
[A78AA][776AA] active transition goes down 1 club (lowjack)
[28276][28776] passive response goes up 1 club
PPSTT vs Maybe to Funky Bookends
[AA776][78776] active transition goes down 1 club (lowjack)
[76287][76787] passive response goes up 1 club
Funky Bookends To PPSTT vs Maybe
[78776][AA776] active transition goes up 1 club (hijack)
[76787][76287] passive response goes down 1 club
PPSTT vs Maybe to PHTTT vs 5 Club Y Not
[776AA][A78AA] active transition goes up 1 club (hijack)
[28776][28276] passive response goes down 1 club
Hijacking in period 7
This the real bleeding edge of where hijacking is at the end of 2019. Over the year I managed to achieve a proof of principle for hijacking in period 7. Not having any particular system for generating hijacks I quite probably have not started with easy patterns. One thing I did find while trying to compose these hijacks is that there is numerical issue making it hard to start with 6 clubs and go to 7vs5 because the passes are 9s. I’m not saying there aren’t any 6 club period 7 hijacks just that they are tough to find. Similarly I found it useful to put some 7s into the patterns even though these are not hijackable passes in these patterns they keep the patterns pleasingly linked when there is only one 9 (I was not in favour of a seven count pattern).
Hijacking out of 9788827 a.k.a period 7 hijacking 1
As far as I am aware none of these patterns have names so they go by their globals in the section headings. The 6 club pattern is a very good test of how metronomic your juggling is in patterns with zips. If it the timing is not metronomic it makes the 6 club pattern remarkably difficult to the extent that in some practices, a partner and I struggled when we were both doing the 6 club pattern for practice, but with the same partner it was much smoother when they were doing the 8 club pattern against me doing the 6 club pattern.
9788827 to 9797226 vs 9797888
[8298877]4[9926772] active transition goes down 1 club (lowjack)
[8778298][8778998]
9797226 vs 9797888 to 9788827
[9926772]6[9887782] active transition goes up 1 club (hijack)
[7789988][7782988]
Hijacking out of 9968827 a.k.a period 7 hijacking 2
As with the previous set of patterns, I don’t think any of these have names. Also, the 6 club pattern is challenging – quite probably also due to minor timing errors that can be introduced when zipping which can become major timing errors as this 6 club pattern has a zip flip locally.
There is no video for this one yet, but all the transitions have been implemented so I can say with confidence that they are correct. It would be nice to have a theory way of finding these transitions and/or proving their correctness!
9968827 to 9922497 vs 9968897
[8296879]4[9924792] active transition goes down 1 club (lowjack)
9922497 vs 9968897 to 9968827
[9924792]6[9687982] active transition goes up 1 club (hijack)
Feedback, additions and corrections
I had hoarded some of the new material for too long waiting to find and publish the elegantly generative rules for generating hijacks. Writing this post has helped things along a little bit, but it is time to share what I have and give others a leg up on tackling the theory challenge. Some of it is not great, but I wanted to get things out rather than waiting for them to be perfect.
I would hope this entire post is error free, but it is pretty long, so it seems reasonable there will be a mistake or two I haven’t caught somewhere. If you find any errors, particularly in the active transitions, please let me know ASAP. If you can suggest what should be there, all the better.
Personally, I would use programming moregenerally to cover forced pattern transitions that don’t fall into similar rules as you mentioned before.
There are a couple of classic ones that don’t fall in to your axioms – although they do have a hijacky feel:
777726 as a global, the ppz side can throw 1 self after (i.e. one round of 7777266 globally) to force a natural feeling transition.
A similar pattern, based on Martin’s one count: if one person has the rule of ‘zip if can, else pass’ , the programmer can do any of ‘ph’ ‘pps’ ‘pppf’ ‘ppppz’ ‘ppppp0’ and have the partner respond.
Transitions into and out of various Jim’s patterns I would class as natural feeling programming patterns that are not hijacking.